はじめに

こんにちは、カンムでバンドルカードの機械学習部分を担当している fkubota です。(ちなみに機械学習エンジニアめっちゃ探してます👀)
前回の記事から日が経ってしまいました。
あれから、沖縄に移住する(2月に)などプライベートで大きめのイベントが多発して忙しく過ごしていました。
そのせいもあり新しい技術に触れるような時間が少なくてなかなかテックブログネタが思いつかなかったのですが、朝会で不便を感じていたのでテックでいい感じにしたろ!と思い立ち勢いで書きます。
前回の記事も朝会についてでした。 カンム流『朝会』をやってみたら予想以上にウケが良かった件
ざっと概要を話すと、
- リモートで雑談減ったよね
- 雑談する会を設けても継続的に行うことって難しいよね
- 新しく入社した人が関係構築するのも難しいよね
という思いから、飽きない、形骸化しづらいしくみの朝会を開催しました。
2021年6月ごろにはじめて未だに(2022年03月31日現在) 続いているのでなかなか悪くない仕組みでは?と思っています。
仕組みは簡単で、
- 週に2回、朝15分開催
- メンバーは毎回ランダム(現在は18人から5人選ぶ感じ)
- 聞き専禁止
- テーマなしの雑談
という感じです。
短いこととランダムなことが効いて飽きづらい仕組みにしています。
biz寄りの人もいればデザイナーもいて普段仕事で会話しない人とも会話できて楽しいです:)
もうすこしいい感じにしたい朝会

この朝会を運用していてもう少しいい感じにしたいなぁと思うことがありました。
ランダムにメンバーを選んでいるのですが、あれーあの人全然選ばれてないなぁとかあの人とあの人が一緒の会に参加してるの見たこと無いなぁとかそんなことを思っていました。
20回参加している人もいれば、5回しか参加していない人もいます。
AさんとBさんはそれぞれ10回参加していますが、同時に参加したことは0回だったりもします。
朝会は月に多くても 10回程度しか開催されないので、そういう状況はまあありえますよね。
問題の形

現在の悩みのタネは
- 全員の参加回数に偏りがある
- 同時に会に参加したことのないペアが存在する
です。
前者だけであれば、簡単にできそうなのですがペアまで考慮するとちょっと複雑そうです。
こういう制約のある数理最適化問題みたいのって存在しそうなんですが、僕は詳しくないので知りません。
なにか知っている人いたらコメントで教えて下さい。
確率モデルを導入して解いてみる
ということで確率モデルを導入してみます。
確率モデルというと仰々しいですがそんなにかっこよくて難しい話ではありません。
もう少しお付き合いいただくとわかってくるかと思います。
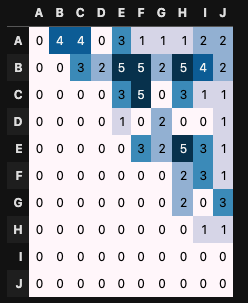
僕は、問題を解くための土台として以下のような表を用意しました。

これは、A~Jの10人のメンバーが朝会に参加した記録です。
10人から3人が朝会に参加するとします。
[A, B, E] が選ばれた場合、表の A行B列、A行E列、B行E列のセルに1が加算されます。
A行B列とB行A列のセルは同等な意味を持ちますので上三角部分だけが意味を成します。
上の表を導入して話を進めていきます。
次に朝会を30回行った場合を見ていきます。
メンバーはランダムに選びます。(pythonで実装しています。)
1回目

5回目
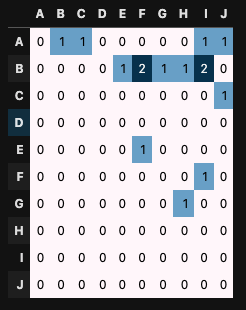
15回目
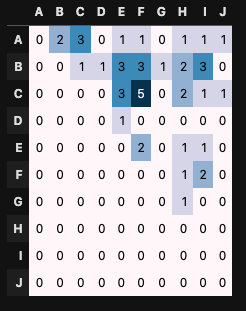
30回目

こんな感じになりました。
BさんとEさん(B行E列)は5回同じ朝会に参加していますが、AさんとDさんは一度も同じ会に参加していません。
各人の合計参加回数はどうでしょうか?
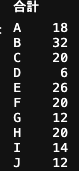
となっており、明らかに偏りがあります。
Bさんの32回に対してDさんは6回なので、参加回数に5倍も差がありますね。
これはなんとかしたいところ。
やりたいことは明らかで、この参加回数表の値が小さいところが選ばれやすいような確率モデルを導入すればいいだけです。
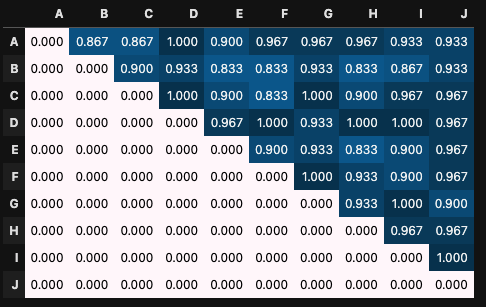
現在のランダムな状況をモデルとして考えると、以下のようになります。
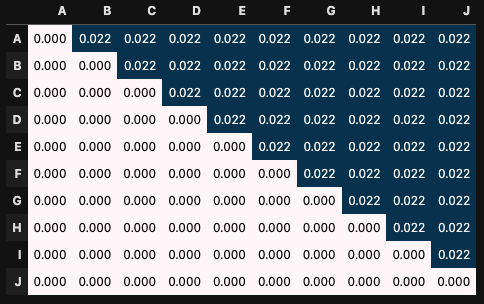
各セルの値が選ばれやすい確率を表しており、すべてのペアを等しい確率で選んでいるので0.022で一定値です。
ちなみにすべてのセルを足すと1になるように正規化しています。 100をかければ%になるので、 0.022×100 = 2.2%なのですべてのペアは2.2%の確率で選ばれます。
このすべて同じ値の表(確率モデル)を改良して、すべてのペアでバランス良く朝会を実現しようというのが今回解いている問題です。
ここまでこれば後は解けたようなものですね。
サクッとやってしまいましょう。
まずは、各セルの値ごとに 朝会に参加していない度 を定義したいと思います。
各セルの参加回数を 、全体の朝会開催数を
とします。
以下のような指標はどうでしょうか?
が定数(今回だと30)なので、
が大きいほど、上の指標
は小さくなります。
つまりペアが実現した回数が大きいほど小さくなります。 朝会参加していない度 として使えそうです。
実際にセルに当てはめてみます。
参加回数表
上記から計算した
回数が少ないほど、 が大きな 大きな値を取っています。
例えば、 だと
であり、
だと
となっています。
しかし、0回と5回で極端に差が開いているのに、1/0.833 ≒ 1.2 と仮に確率として扱うと、1.2倍程度しか差がなくて微妙です。
もう少し、回数の差に対して勾配をつけたいです。さらには、その勾配加減を調整できると嬉しいです。
実現方法はいくらでもありますが、僕は 指数関数を用いることにしました。
新しく定義する 朝会参加していない度 を とします。
ここで、 は
の実数であり、
が大きいときには
が小さい場合、
をより小さく、大きい時より大きくします。(勾配をコントロールします)
の場合と
の場合の
を見てみましょう。
の場合
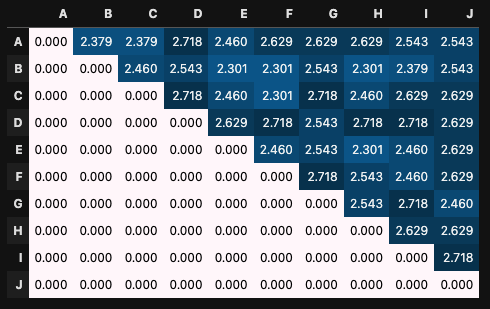
の場合

のほうが
の値の大きさに激しく値が反応している事がわかります。
あとは、これを正規化(すべてのセルを足して1にする)して確率 として扱います。
という式になり、おなじみにの softmax関数となりました。
作ったモデルで遊んで見る
作ったモデルで実際にシミュレーションしてみます。
朝会のメンバーを選ぶプロセスは
- 参加回数表から確率の表を作成
- 表を元に3人の参加者を選ぶ
- 表を更新
- 1~3を繰り返す
とこんな感じです。
- randomに選ぶパターン
で選ぶパターン
で選ぶパターン
をやってみました。
朝会の開催回数うは としています。
結果は
random
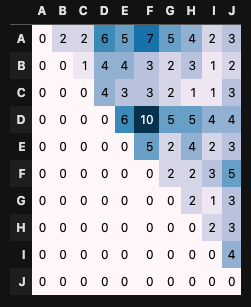
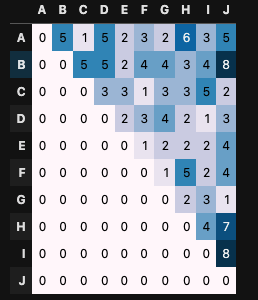 ]
]
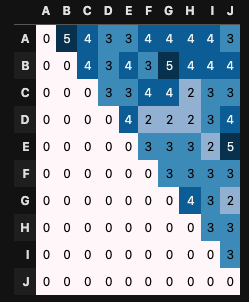
となり、 が大きいほど極端に多い/少ないが見られません。
意図した動作になっているようです。
ちなみに、 の終了時の確率の表は以下のようになっていました。

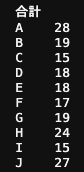
また、参加合計回数を randomと で比較すると
のほうが公平に参加できている事がわかります。
ramdom
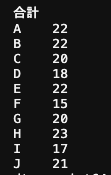
評価してみる
上述したように によって、参加回数をコントロールできるようになり、参加回数表も均一になっているように見えます。
どの程度均一になっているのか?を定量的に評価したくなったのでこれもやってみました。
まあ、分散でいいだろうと思ったのでちゃちゃっと計算した結果を見せます。
分散は、参加回数表の各セルの平均値を、セル数を
とした時以下のような式で表されます。
横軸に朝会の開催回数、縦軸に を取ったグラフを書きました。
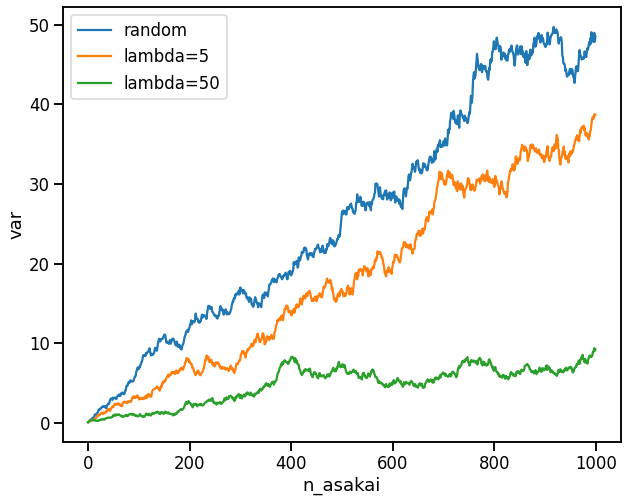
こちらもが大きいほど分散が小さいことがわかります。
意図した動作が実現できています。
おわり
以上です。
なんか朝会ガチ勢みたいな記事になってしまって申し訳ないですが、最後まで見てくださってありがとうございます。
頑張って考えましたが実践導入するかちょっと迷います。
めんどくさくなっちゃうといけないので、そこまでのメリットがあるのかは要検討です。
とはいえ、自分で問題を作って解くというはやっぱり面白いなと思いました。
結構楽しめてよかったです。
第二弾があるかはわかりませんが、面白そうな事ができそうならチャレンジしてみたいです。
定番ですが、積極採用中です!
機械学習エンジニアをめっちゃ探してますのでカジュアル面談からでも何卒!!!!